2-13 預防流感高峰

菊普茶泡好後，看著熱起緩緩蒸騰而上，飛哥指著ACF、PACF圖說道:「看到右邊圖了嗎?在平移第12筆資料的位置是不是有一個高點? 這個就顯現出資料每12個月出現一次循環，左圖的部分說明的是每個時間點與原始資料的相關性高低，所以每12筆資料會出現一個循環，你就可以發現資料是一直上上下下起伏的，暑假期間因為天氣熱導致流感人數少，可以觀察到6~8月的人數會跟11~1月的流感人數成相反的表現，因此呈現負相關。」

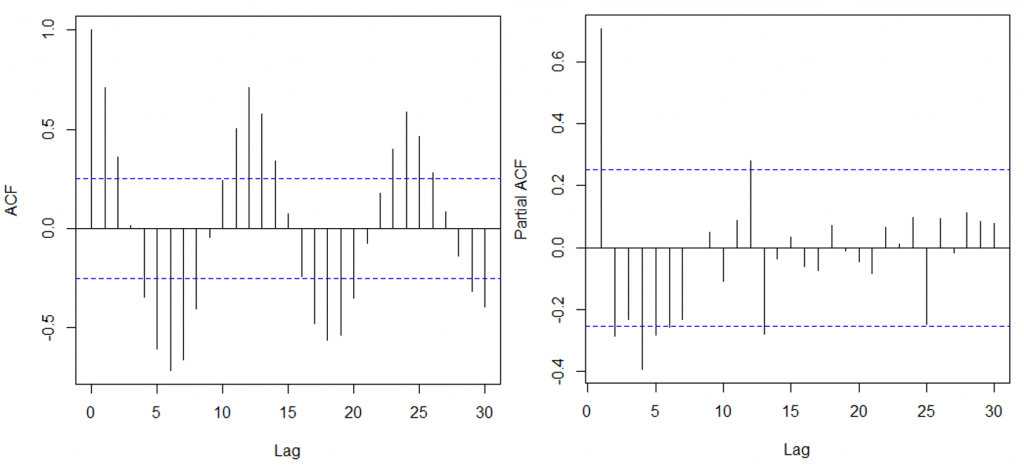
「就上面兩張圖來看的話，ACF的高點可以對應ARIMA的MA部分(一直起伏故不選擇)，PACF的高點可以對應ARIMA的AR部分(這裡選擇4)，又之前提過疾管署的數據相對平穩不需要差分(中間為0)，而資料每12個月一個週期(後方的週期為12)，因此ARIMA模型可以寫成ARIMA(4,0,0)(0,0,1)[12]。」飛哥講完一連串的判斷邏輯後，喝了口剛泡的菊普茶。

小博點了點頭說著:「那有可以自動挑選適合ARIMA數字的程式嗎?」

「有是有，像我現在直接用auto.arima來測試，程式執行完建議的模型是ARIMA(5,0,0)(0,0,0)[0]，可以看出並不建議用12個月的週期來建模型，反而它用了AR(1)~AR(5)來建模，我們測試這個模型的殘差發現它其實並沒有解決12的那個週期，所以說這個程式我比較建議與我們的資料特徵做綜合參考，因此調整後的模型變成ARIMA(5,0,0)(0,0,1)[12]。」飛哥將整個模型選擇的來龍去脈說明了一次。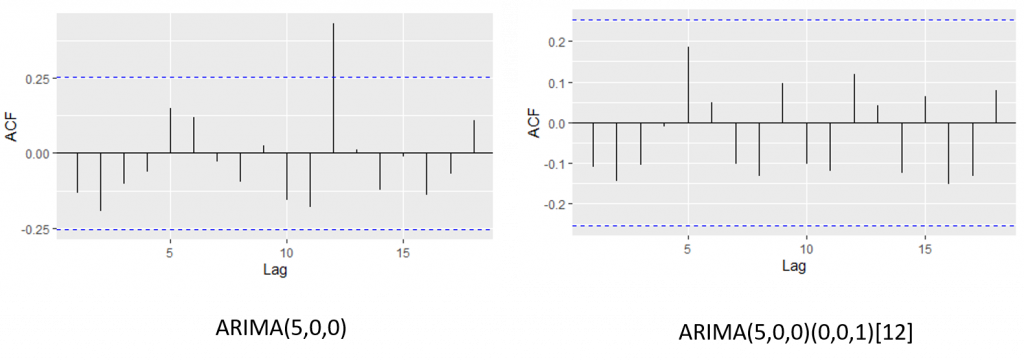

(PACF跟ACF表現相似，故這邊僅放ACF)

小博露出恍然大悟的表情說道:「喔!原來是這樣，我看auto.arima的選擇邏輯是AIC或BIC愈小就愈容易被選為最佳模型，但是它可能並沒有將週期納入第一的考量，反而忽略週期的重要性，因此我們可以把它的程式輸出當作ARIMA數字選擇的參考，對嗎?」

飛哥滿意的笑了笑並說:「沒錯，模型建完後，還可以利用Ljung-box test來測試資料的殘差是否已經沒有週期或規律了，只要P-value < 0.05就可以被認為是統計上的隨機亂數(指隨機產生的誤差量，不具有一定的規律可循)。」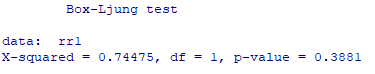

「時間序列真的蠻神奇的耶!雖然它已經被發展很久了，想不到背後的操作還有這麼多可以調整的地方，或許之後找到其他具有自相關的資料集時，可以再拿時間序列來分析看看。」小博在一旁驚嘆著。

飛哥將整理好的資料寄出後，就將剩下的菊普茶喝完，準備出門運動運動，活動筋骨下。

R程式時間

x=c(154,123,79,87,63,54,32,13,28,69,86,75,
    112,100,89,82,76,56,48,21,22,38,73,85,
    139,130,93,90,73,60,44,21,26,47,59,69,
    132,110,99,72,74,52,43,28,29,48,63,75,
    135,120,93,90,66,67,47,31,25,47,69,59)

library(forecast)

fit <- Arima(x, order=c(5,0,0), seasonal=c(0,0,0))
checkresiduals(fit) #確認殘差是否正常

auto.arima(x,seasonal=TRUE) # 自動抓取適合的arima模型

r1=arima(x, order = c(5, 0, 0), seasonal = list(order = c(0, 0, 1), period = 12)) #加入週期模式
rr1=residuals(r1) #取出殘差
checkresiduals(rr1)

Box.test(rr1, type="Ljung-Box") #模型檢測，p-value<0.05表示配完模型後無週期，模型良好

資料參考:
https://medium.com/r-%E8%AA%9E%E8%A8%80%E8%87%AA%E5%AD%B8%E7%B3%BB%E5%88%97/r%E8%AA%9E%E8%A8%80%E8%87%AA%E5%AD%B8%E6%97%A5%E8%A8%98-14-arima%E6%A8%A1%E5%9E%8B%E7%B0%A1%E4%BB%8B%E8%88%87%E5%AE%9A%E9%9A%8E-d1fa7037c53d